어디까지 갈 수 있을까?
chapter 6. 정렬 본문
정렬이란 데이터를 특정한 기준에 따라 순서대로 나열한 것이다.
리스트의 .reverse()는 O(N)의 복잡도로 수행 가능하기 때문에 오름차순 코드만 다루기로 한다.
1. 선택정렬
정렬되지 않은 배열 중 가장 작은 값을 선택해 정렬한다
시간복잡도는 O(N^2) 이다
|
1
2
3
4
5
6
7
8
|
arr=[7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(len(arr)):
min_index=i
for j in range(i+1, len(arr)):
if arr[min_index]>arr[j]:
min_index=j
arr[i], arr[min_index] = arr[min_index], arr[i]
|
cs |
[0, 5, 9, 7, 3, 1, 6, 2, 4, 8]
[0, 1, 9, 7, 3, 5, 6, 2, 4, 8]
[0, 1, 2, 7, 3, 5, 6, 9, 4, 8]
[0, 1, 2, 3, 7, 5, 6, 9, 4, 8]
[0, 1, 2, 3, 4, 5, 6, 9, 7, 8]
[0, 1, 2, 3, 4, 5, 6, 9, 7, 8]
[0, 1, 2, 3, 4, 5, 6, 9, 7, 8]
[0, 1, 2, 3, 4, 5, 6, 7, 9, 8]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
2. 삽입 정렬
데이터를 하나씩 확인하며 각 데이터를 적절한 위치에 삽입한다
시간복잡도는 O(N^2) 이다
|
1
2
3
4
5
6
7
8
|
arr=[7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(1, len(arr)):
for j in range(i, 0, -1):
if arr[j-1]>arr[j]:
arr[j-1], arr[j] = arr[j], arr[j-1]
else:
break
|
cs |
[5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
[5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
[0, 5, 7, 9, 3, 1, 6, 2, 4, 8]
[0, 3, 5, 7, 9, 1, 6, 2, 4, 8]
[0, 1, 3, 5, 7, 9, 6, 2, 4, 8]
[0, 1, 3, 5, 6, 7, 9, 2, 4, 8]
[0, 1, 2, 3, 5, 6, 7, 9, 4, 8]
[0, 1, 2, 3, 4, 5, 6, 7, 9, 8]
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
3. 퀵정렬
기준 데이터를 설정하고 기준보다 큰 데이터와 작은 데이터의 위치를 바꾼다
시간복잡도는 O(nlogn) 이다
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
array=[7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
if len(array)<=1:
return array
pivot=array[0]
tail=array[1:]
left_side = [x for x in tail if x<=pivot]
right_side= [x for x in tail if x>pivot]
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))
|
cs |
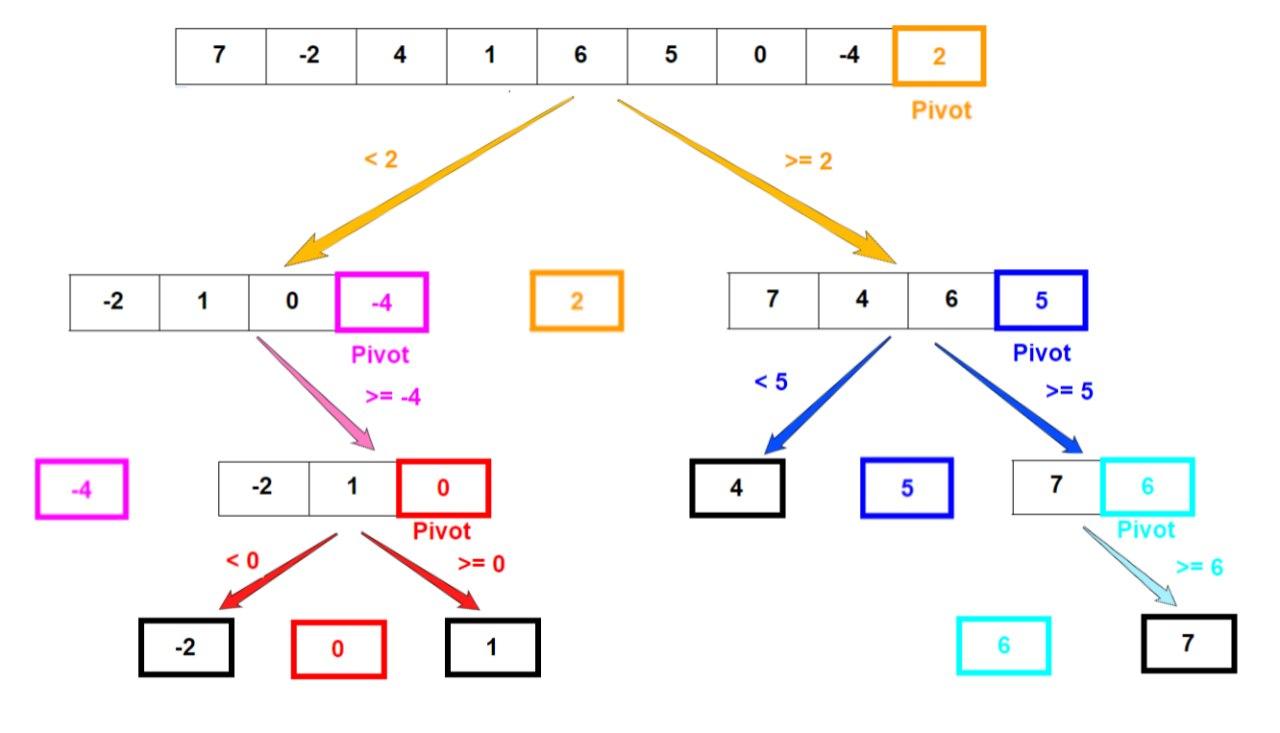
pivot보다 작은 데이터는 left_side에 담고 pivot보다 큰 데이터들은 right_side에 담는 연산을 반복한다

깊이는 약 logn 이고 데이터의 갯수가 n이므로 시간복잡도는 O(nlogn)이 된다
4. 계수정렬
데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때만 사용할 수 있는 알고리즘이다.
시간복잡도는 O(N+K)이다. *N : 데이터의 갯수, K : 데이터의 최댓값
|
1
2
3
4
5
6
7
8
9
10
11
12
|
array=[7, 7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
count=[0]*(max(array)+1)
for i in range(len(array)):
count[array[i]]+=1
print(count) #[1, 1, 1, 1, 1, 1, 1, 2, 1, 1]
for i in range(len(count)):
for j in range(count[i]):
print(i, end=' ') # 0 1 2 3 4 5 6 7 7 8 9
|
cs |
count 라는 새로운 배열을 만들어 array의 값을 count의 인덱스로 받아 특정 array 값의 갯수만큼 count의 값을 증가시킨다
* 파이썬의 정렬 라이브러리
정렬된 배열을 리턴하는 sorted()
리턴값이 없는 sort()가 있다
둘 다 O(NlogN)의 시간복잡도를 보장한다.
|
1
|
mylist.sort(key=lambda x: x[1])
|
cs |
① 위에서 아래로
|
1
2
3
4
5
6
7
8
9
|
import sys
input = sys.stdin.readline
arr=[]
for _ in range(int(input())):
arr.append(int(input()))
arr.sort(reverse=True)
for i in arr:
print(i, end=' ')
|
cs |
② 성적이 낮은 순서로 학생 출력하기
딕셔너리는 sort()가 제공되지 않으므로 sorted()를 쓰자
|
1
2
3
4
5
6
7
8
9
10
11
12
|
import sys
input = sys.stdin.readline
dict={}
for _ in range(int(input())):
a, b = input().split()
dict[a] = int(b)
sorted_dict = sorted(dict.items())
for c, d in sorted_dict:
print(c, end=' ')
|
cs |
③ 두 배열의 원소 교체
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
import sys
input = sys.stdin.readline
# 원소 개수, 바꿔치기 연산
n, k = map(int, input().split())
# arr 크게 만들기
arr=list(map(int, input().split()))
brr=list(map(int, input().split()))
arr.sort(reverse=True)
brr.sort()
for count in range(1, k+1):
if arr[-count] < brr[-count]:
arr[-count], brr[-count] = brr[-count], arr[-count]
else:
break
print(sum(arr))
|
cs |
'알고리즘 > 이것이취업을위한코딩테스트다' 카테고리의 다른 글
| chaper 7. 이진 탐색 (0) | 2021.02.19 |
|---|---|
| 정렬 문제 (0) | 2021.02.17 |
| DFS/BFS 문제 (0) | 2021.02.15 |
| chapter 5. DFS/BFS (0) | 2021.02.13 |
| 그리디, 구현 문제 (0) | 2021.02.13 |


